Abstract
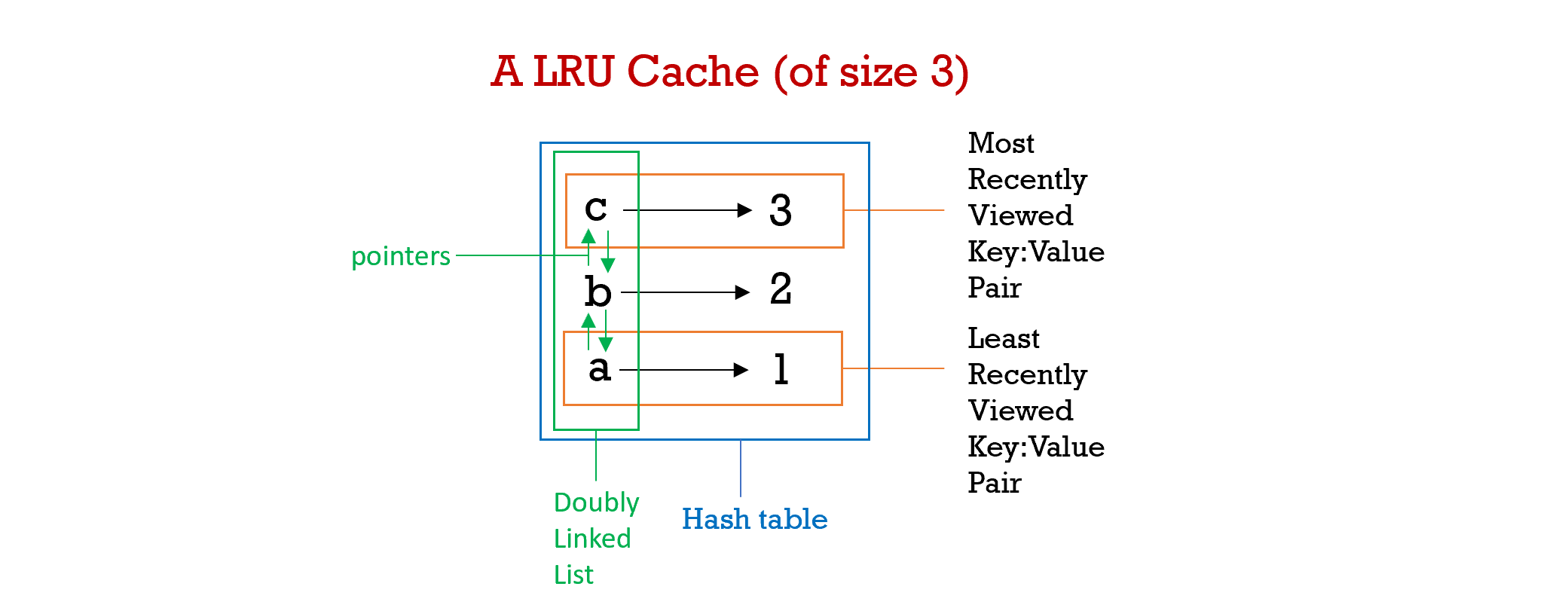
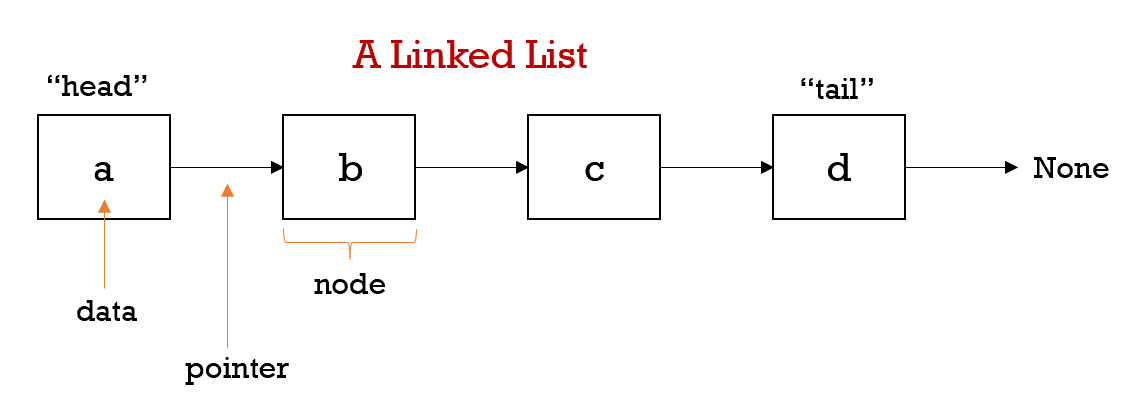
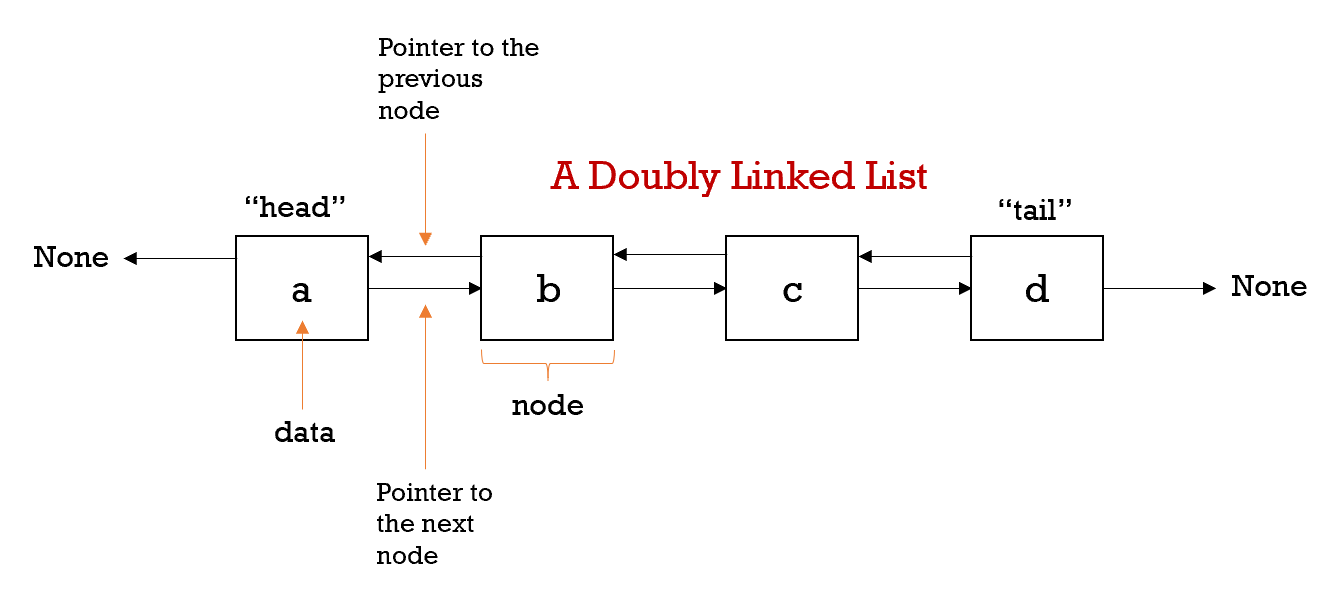
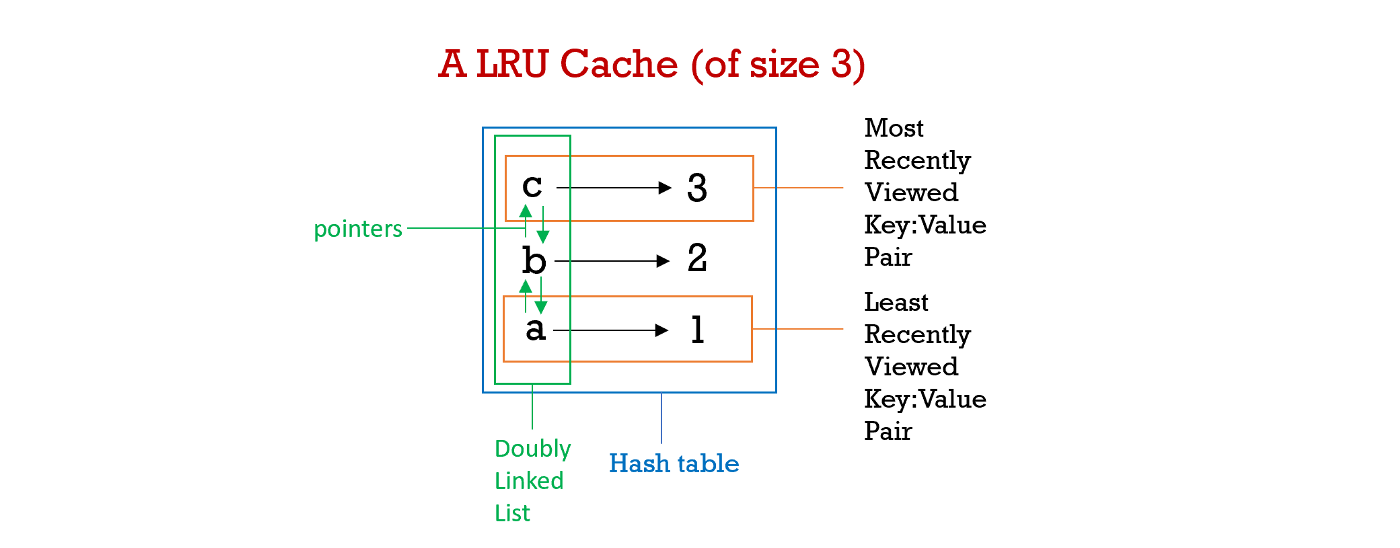
Hash Tables > Linked List > Doubly Linked List > Build your own LRU Cache
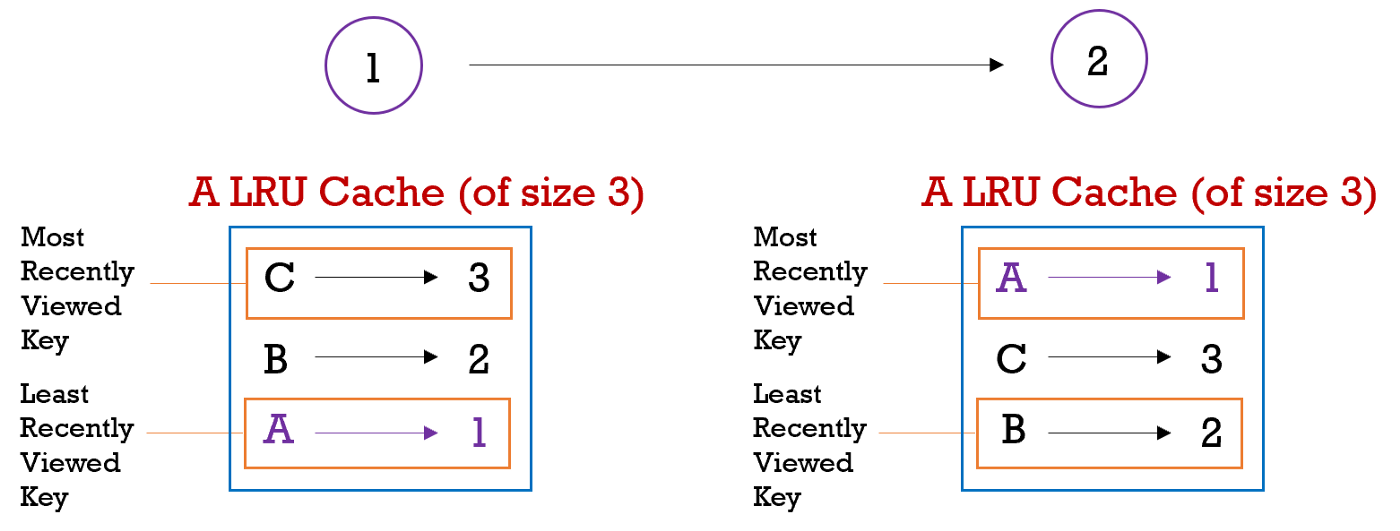
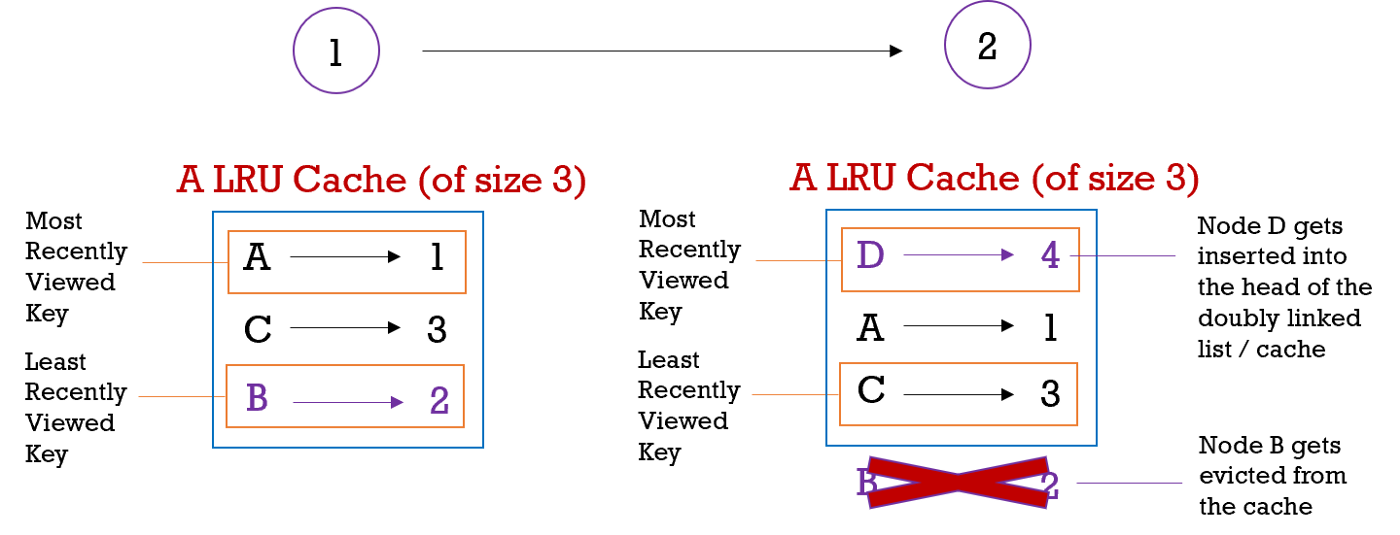
This article covers two key data structures (Doubly Linked List & Hash tables) that are essential for the basic development of an LRU cache, it will discuss the codes that are involved, and guide you through the thought process of building one on your own. The purpose of a cache is to enable fast data retrieval through recently used resources reducing the reliance on the computer's main memory source.